0x00 RSA算法简述
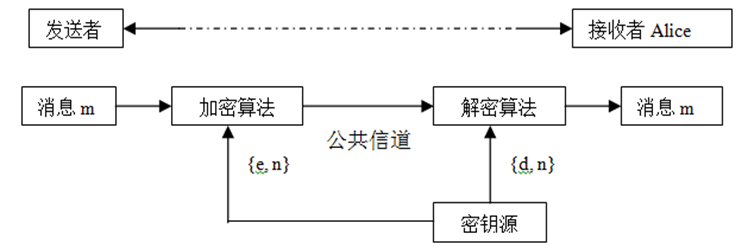
密钥的产生
① 选择两个满足需要的大素数p和q,计算n=p×q,φ(n)= (p-1)×(q-1),其中φ(n)是n的欧拉函数值。
② 选一个整数e,满足1<e<φ(n),且gcd(φ(n),e)=1。通过d×e≡1modφ(n),计算出d。
③ 以{e,n}为公开密钥,{d,n}为秘密密钥。
假设Alice是秘密消息的接收方,则只有Alice知道秘密密钥{d,n},所有人都可以知道公开密钥{e,n}。
加密
如果想发送消息m给Alice,就选择Alice的公钥{e,n},然后计算:$c≡m^e mod n$,然后把c发送给Alice。
解密
接收方Alice收到c,用私钥计算:$m≡c^dmodn$
- 能够抵御选择明文攻击
- RSA的安全性基于分解大整数难题
(1)不同的用户不能用相同的模数n. 大素数的个数是十分庞大的资源,不用担心会被用完。
(2)p与q的差值要大
(3)p-1和q-1都应有大的素因子。
(4)私钥d的选择。如果私钥d的值比较小,由RSA的解密算法可知,对数据进行解密的速度越快。但是,私钥d的值不能太小,一般要求d≥n1/4。
(5)更换密钥
如果私钥d被泄露,则在模n的情况下重新计算一对密钥是不够的,而是必须选择一个新的公钥n.
(6)e不可太小,否则不安全。
0x01 数据处理
基本上来说,RSA的题目都是围绕着c,m,e,d,n,p,q这几个参数展开的,但是题目一般不会直接给这种样子的参数,而是通过别的方式给出,这里就需要我们使用一些工具或者自己手工将这些参数提取出来。
pem文件:针对此类文件可以直接使用openssl提取,大概使用过的方式有:
1 | ```openssl rsa -pubin -text -modulus -in warmup -in public.pem |
pcap文件:针对此类文件可以使用wireshark follow一下。这种问题一般都是写了一个交互的crypto系统,所以可能产生多轮交互。
PPC模式:这种模式是上述pcap文件的交互版,会给一个端口进行一些crypto的交互,参数会在交互中给出。
0x02 模数分解
解决RSA题目最简单,最暴力,最好使的方法就是分解模数n。拿到题目先尝试能否将n分解成功,若成功得到p,q的取值,那么可求n的欧拉函数的值。
$$ varphi(n)=(p-1)(q-1) $$
0x03 低加密指数攻击
介绍
e又被称为加密指数,选取小一点的e可以缩短加密时间,但是选取不当的话,就会造成安全问题。
推荐在e=3时首先尝试此方法
当e=3时,如果明文过小,导致明文的三次方仍然小于n,那么通过直接对密文三次开方,即可得到明文。
如果e=3,且$ m^e<{n} $,那么$ c= m^e,$ $e=3$,即:
$$ m = sqrt[3]{c} $$
如果明文的三次方比n大,但是不是足够大,那么设k,有:
$$ c= m^e+kn $$
爆破k,如果$ c-kn $能开三次根式,那么可以直接得到明文。
例题
安恒月赛
e = 3
n=0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793L
c=0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
解密脚本
1 | import gmpy2 |

gmpy2.iroot(m, n)函数:获取m开n次方的结果,返回一个tuple,第一个数为结果,第二个数为是否为整数的布尔值。